Rotazione nel piano complesso

Per studiare la rotazione nel piano complesso si possono distinguere due casi, dipendentemente dal fatto che il centro di tale rotazione sia rappresentato dall'origine del sistema di riferimento o da un qualsiasi altro punto.

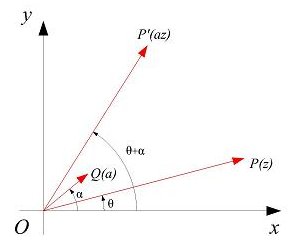
Sia ${\displaystyle a}$ un numero complesso di modulo unitario:

${\displaystyle a=\cos \vartheta +i\sin \vartheta =e^{i\vartheta }}$

e sia ${\displaystyle z}$ un qualsiasi numero complesso

${\displaystyle z=\rho (\cos \varphi +i\sin \varphi ).}$

La rotazione di centro l'origine degli assi ${\displaystyle O}$ e di ampiezza ${\displaystyle \vartheta }$, ${\displaystyle \vartheta \in \mathbb {R} }$, è la trasformazione:

${\displaystyle {\begin{aligned}\rho _{O,\vartheta }\colon \mathbb {C} &\longrightarrow \mathbb {C} \\z&\longmapsto z'=az=e^{i\vartheta }z\end{aligned}}}$

che associa al punto ${\displaystyle P(z)}$, corrispondente di ${\displaystyle z}$, il punto ${\displaystyle P'(z')}$, corrispondente del numero complesso ${\displaystyle z'=az}$, di modulo uguale al modulo di ${\displaystyle z}$, ${\displaystyle \rho }$, e di argomento ${\displaystyle \varphi +\vartheta }$.

Si osservi che, nella definizione appena data, ${\displaystyle \vartheta }$ può assumere qualsiasi valore reale, incluso lo ${\displaystyle 0}$ e i valori negativi.

Dalla definizione, data, segue che le rotazioni del piano complesso formano un gruppo abeliano rispetto alla composizione.

I numeri complessi di modulo unitario formano un gruppo moltiplicativo, chiamato gruppo circolare. È facile dedurre che esso è algebricamente isomorfo al gruppo delle rotazioni nel piano complesso: basta associare a ogni complesso unitario ${\displaystyle a}$ del gruppo circolare, la rotazione complessa definita da ${\displaystyle z\mapsto az}$.

Infatti:

${\displaystyle z'=az=\rho (\cos \varphi +i\sin \varphi )(\cos \vartheta +i\sin \vartheta )=\rho [\cos(\varphi +\vartheta )+i\sin(\varphi +\vartheta )]=\rho e^{i(\varphi +\vartheta )}.}$

Passando in coordinate cartesiane e ricordando la forma delle equazioni che determinano la rotazione di centro l'origine degli assi cartesiani e angolo ${\displaystyle \vartheta }$:

${\displaystyle \rho _{O,\vartheta }:{\begin{cases}x'=x\cos \vartheta -y\sin \vartheta \\y'=x\sin \vartheta +y\cos \vartheta .\end{cases}}}$

Si ha che:

moltiplicare il numero complesso ${\displaystyle z}$ per un numero complesso ${\displaystyle a}$ di modulo unitario, equivale ad applicare nel piano al punto ${\displaystyle P(z)}$ una rotazione avente come centro l'origine degli assi e angolo ${\displaystyle \vartheta }$, con ${\displaystyle \vartheta \in \mathbb {R} }$.

Notiamo che:

• Se l'angolo di rotazione è pari a ${\displaystyle 0}$, o a un multiplo di ${\displaystyle 2\pi }$, la relativa rotazione lascia invariato ogni punto del piano complesso: si tratta della trasformazione identica.

• La rotazione corrispondente a ${\displaystyle \vartheta +\varrho }$ equivale alla composizione delle due rotazioni individuate da ${\displaystyle \vartheta }$ e ${\displaystyle \varrho .}$

• La rotazione corrispondente a ${\displaystyle -\vartheta }$, è l'inversa della trasformazione corrispondente a ${\displaystyle \vartheta }$: la loro composizione dà infatti la trasformazione identica.

Le tre proprietà elencate permettono di dedurre che l'associazione di un numero reale ad una rotazione, definisce un'applicazione lineare tra il gruppo abeliano dei numeri reali (con l'usuale operazione di somma) e il gruppo delle rotazioni del piano complesso (dotato dell'operazione di composizione tra funzioni). L'applicazione lineare così definita non è un omomorfismo, difettando infatti della non biunivocità.

La trasformazione che ammette come scrittura complessa

${\displaystyle z'=\left(-{{\sqrt {2}} \over 2}+i{{\sqrt {2}} \over 2}\right)z}$

è una rotazione attorno all'origine degli assi di angolo ${\displaystyle \vartheta ={3 \over 4}\pi }$.

Infatti:

${\displaystyle -{{\sqrt {2}} \over 2}+i{{\sqrt {2}} \over 2}=\cos \left({3 \over 4}\pi \right)+i\sin \left({3 \over 4}\pi \right)=e^{i{3 \over 4}\pi },}$

quindi

${\displaystyle z'=\left(-{{\sqrt {2}} \over 2}+i{{\sqrt {2}} \over 2}\right)z=e^{i{3 \over 4}\pi }z}$

è una rotazione attorno all'origine degli assi cartesiani di angolo ${\displaystyle \vartheta ={3 \over 4}\pi }$.

• Se l'angolo di rotazione è uguale a ${\displaystyle \pi /2}$, allora

${\displaystyle a=e^{i{\pi \over 2}}=\cos \left({\pi \over 2}\right)+i\sin \left({\pi \over 2}\right)=i.}$

Quindi: la rotazione di centro l'origine degli assi ${\displaystyle O}$ e di ampiezza ${\displaystyle \pi /2}$ coincide con la moltiplicazione per l'unità immaginaria ${\displaystyle i}$:

${\displaystyle {\begin{aligned}\rho _{O,{\pi \over 2}}\colon \mathbb {C} &\longrightarrow \mathbb {C} \\z&\longmapsto z'=e^{i{\pi \over 2}}z=iz.\end{aligned}}}$

Infatti, indicando con

${\displaystyle z=\rho (\cos \varphi +i\sin \varphi )}$

si ha che:

${\displaystyle z'=iz=\rho \left[\cos \left(\varphi +{\pi \over 2}\right)+i\sin \left(\varphi +{\pi \over 2}\right)\right]=\rho e^{i\left(\varphi +{\pi \over 2}\right)}.}$

• Se l'angolo di rotazione è pari a ${\displaystyle \pi }$, allora

${\displaystyle a=e^{i\pi }=\cos \left(\pi \right)+i\sin \left(\pi \right)=-1.}$

Quindi la rotazione di centro l'origine degli assi ${\displaystyle O}$ e di ampiezza ${\displaystyle \pi }$ è data da:

${\displaystyle {\begin{aligned}\rho _{O,{\pi }}\colon \mathbb {C} &\longrightarrow \mathbb {C} \\z&\longmapsto z'=e^{i\pi }z=-z.\end{aligned}}}$

Infatti, indicando con

${\displaystyle z=\rho (\cos \varphi +i\sin \varphi ),}$

si ha che:

${\displaystyle z'=-z=\rho \left[\cos \left(\varphi +\pi \right)+i\sin \left(\varphi +\pi \right)\right]=\rho e^{i\left(\varphi +{\pi }\right)}.}$

Quindi la rotazione di centro l'origine degli assi ${\displaystyle O}$ e di ampiezza ${\displaystyle \pi }$ equivale alla simmetria rispetto all'origine.

• Se l'angolo di rotazione è uguale a ${\displaystyle {3 \over 2}\pi }$, allora

${\displaystyle a=e^{i{3 \over 2}\pi }=\cos \left({3 \over 2}\pi \right)+i\sin \left({3 \over 2}\pi \right)=-i.}$

Quindi la rotazione di centro l'origine degli assi ${\displaystyle O}$ e di ampiezza ${\displaystyle {3 \over 2}\pi }$ è:

${\displaystyle {\begin{aligned}\rho _{O,{3 \over 2}\pi }\colon \mathbb {C} &\longrightarrow \mathbb {C} \\z&\longmapsto z'=e^{i{3 \over 2}\pi }z=-iz.\end{aligned}}}$

Infatti, indicando con

${\displaystyle z=\rho (\cos \varphi +i\sin \varphi ),}$

si ha che:

${\displaystyle z'=-iz=\rho \left[\cos \left(\varphi +{3 \over 2}\pi \right)+i\sin \left(\varphi +{3 \over 2}\pi \right)\right]=\rho e^{i\left(\varphi +{3 \over 2}\pi \right)}.}$

Sia ${\displaystyle C_{0}=P(z_{0})}$ il punto corrispondente al numero complesso ${\displaystyle z_{0}=x_{0}+iy_{0}}$, e sia ${\displaystyle a}$ un numero complesso di modulo unitario.

La rotazione di centro ${\displaystyle C_{0}(x_{0};y_{0})}$ e angolo ${\displaystyle \vartheta }$, ${\displaystyle \vartheta \in \mathbb {R} }$ è data da:

${\displaystyle {\begin{aligned}\rho _{C_{0},{\vartheta }}\colon \mathbb {C} &\longrightarrow \mathbb {C} \\z&\longmapsto z'=az+b=e^{i\vartheta }z+b,\end{aligned}}}$

con ${\displaystyle b=(1-a)z_{0}}$.

Infatti se moltiplicare il numero complesso ${\displaystyle z}$ per un numero complesso ${\displaystyle a}$ di modulo unitario, equivale ad applicare al punto ${\displaystyle P(z)}$ una rotazione di centro l'origine degli assi e angolo ${\displaystyle \vartheta }$, ${\displaystyle \vartheta \in \mathbb {R} }$, considerando il punto ${\displaystyle C_{0}}$ come nuova origine degli assi, si ha che ${\displaystyle z'-z_{0}=a(z-z_{0})}$, quindi ${\displaystyle z'=az+(1-a)z_{0}}$.

Ponendo ${\displaystyle b=(1-a)z_{0}}$ si ottiene il caso generale della rotazione.

Per determinare la scrittura complessa della rotazione di centro ${\displaystyle C_{0}(-2-i)}$ e angolo ${\displaystyle \vartheta ={\pi \over 2}}$ si osservi che il centro della rotazione ${\displaystyle C_{0}(-2-i)}$ è il punto associato al numero complesso ${\displaystyle z=-2-i}$.

Quindi, ricordando che ${\displaystyle b=(1-a)z_{0}}$, si ha che

${\displaystyle z'=e^{i\vartheta }z+b=e^{i{\pi \over 2}}z+(1-i)(-2-i)=iz+(-2-i+2i-1)=iz+(-3+i),}$

cioè la trasformazione data da:

${\displaystyle {\begin{aligned}\rho _{(-2-i),{\pi \over 2}}\colon \mathbb {C} &\longrightarrow \mathbb {C} \\z&\longmapsto z'=iz+(-3+i).\end{aligned}}}$

• Rotazione (matematica)
• Trasformazione geometrica piana