Théorème de Varignon

Il existe deux théorèmes démontrés par Pierre Varignon.

Théorème mathématique

Théorème — Si ABCD est un quadrilatère quelconque et I, J, K, L les milieux de ses côtés, alors IJKL est un parallélogramme^[1].

D'autre part, si ABCD est plan et convexe, son aire est le double de celle de IJKL.

En corollaire, les médianes d'un quadrilatère ont même milieu (étant les diagonales du parallélogramme).

Le périmètre du parallélogramme de Varignon est égal à la somme des longueurs des diagonales du quadrilatère.

Démonstration

Par application du théorème des milieux, on montre que les côtés opposés de IJKL sont chacun parallèle à une diagonale de ABCD, donc parallèles entre eux.

D'après le théorème de Thalès, la base b de IJKL est égale à la moitié de la diagonale d de ABCD, et la hauteur h est égale à la moitié de la hauteur h’ prise d'un sommet à l'autre de ABCD (perpendiculairement à la diagonale).

Donc $Aire(ABCD)={\frac {1}{2}}\times d\times {h^{\prime }}={\frac {1}{2}}\times 2b\times 2h=2\times Aire(IJKL)$ .

Une démonstration algébrique du théorème de Varignon

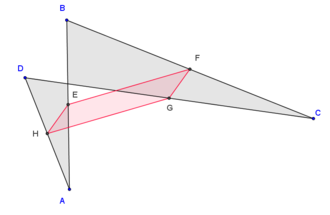
En reprenant les notations du dessin ci-dessus, et en adoptant les notations barycentriques, on a :

I={\frac {1}{2}}(A+B),\,J={\frac {1}{2}}(B+C),\,K={\frac {1}{2}}(C+D),\,L={\frac {1}{2}}(A+D)

donc (par associativité du barycentre)

{\frac {1}{2}}(I+K)={\frac {1}{4}}(A+B+C+D)={\frac {1}{2}}(J+L)

ce qui exprime que IJKL est un parallélogramme.

Cette démonstration illustre la « jolie métaphore » de Nicolas Bourbaki, rapportée par Georges-Théodule Guilbaud dans son avant propos d'un livre de Hermann Weyl^[2] : « Sous cette impitoyable clarté (celle de l'algèbre), la géométrie classique se fane brusquement et perd son éclat. »

En outre, elle dissipe toute hésitation concernant les quadrilatères croisés ou les quadrilatères concaves.

Théorème mécanique

Une force ${\vec {F}}$ se décompose en deux forces ${\vec {F}}_{1}$ et ${\vec {F}}_{2}$ :

{\vec {F}}={\vec {F}}_{1}+{\vec {F}}_{2}

Le théorème de Varignon énonce que

le moment de la force

{\vec {F}}

par rapport à un point est égal à la somme des moments de forces

{\vec {F}}_{1}

{\vec {F}}_{2}

par rapport à ce même point,

si l'on considère un point A quelconque :

M_{{\vec {F}}/A}=M_{{\vec {F_{1}}}/A}+M_{{\vec {F_{2}}}/A}

(en valeur algébrique),

ou bien

{\vec {M}}_{{\vec {F}}/A}={\vec {M}}_{{\vec {F_{1}}}/A}+{\vec {M}}_{{\vec {F_{2}}}/A}

(en vectoriel)

Cas particuliers

Le parallélogramme de Varignon est un losange si et seulement si les deux diagonales du quadrilatère ont la même longueur, c'est-à-dire si le quadrilatère est un quadrilatère équidiagonal.

Le parallélogramme de Varignon est un rectangle si et seulement si les diagonales du quadrilatère sont perpendiculaires, c'est-à-dire si le quadrilatère est un quadrilatère orthodiagonal.

Avec un quadrilatère croisé, le parallélogramme de Varignon peut dégénérer en quatre points colinéaires, formant un segment de droite parcouru deux fois. Cela se produit lorsque le polygone est formé en croisant les deux côtés parallèles d'un trapèze comme dans un antiparallélogramme.

Références

↑ Jean Dieudonné, Algèbre linéaire et géométrie élémentaire, Paris, Hermann, coll. « Enseignement des sciences », 1964, ex. 2, p. 50.
↑ Hermann Weyl (trad. de l'anglais), Symétrie et mathématique moderne, Paris, Flammarion, 1996 (1^re éd. 1964), 151 p. (ISBN 2-08-081366-8, OCLC 36104865).