Teorema del sinus

En trigonometria, el teorema del sinus és una afirmació respecte d'un triangle qualsevol en el pla, vàlida també per un triangle esfèric i amb una formulació equivalent a la geometria hiperbòlica. Si els costats d'un triangle són a, b i c i els angles oposats a aquests costats són A, B i C, llavors el teorema del sinus afirma:

${\displaystyle {\frac {a}{\sin A}}={\frac {b}{\sin B}}={\frac {c}{\sin C}}=2R}$

on R és el radi de la circumferència circumscrita en el triangle. Aquest teorema és útil per a calcular els altres dos costats d'un triangle quan es coneixen dos angles i un costat, un problema habitual en la tècnica de triangulació. També es pot fer servir quan es coneixen dos costats i un dels angles que no és el comprès entre els dos costats; en aquest cas, la fórmula pot donar dos valors possibles per a l'angle comprès. Quan això passa, sovint només un dels resultats farà que tots els angles siguin més petits de 180°; en altres casos, hi ha dues solucions vàlides per al triangle (vegeu la secció el cas ambigu d'aquest mateix article per a més informació).

Es pot demostrar que

${\displaystyle {\begin{aligned}2R={\frac {abc}{2A}}&{}={\frac {abc}{2{\sqrt {s(s-a)(s-b)(s-c)}}}}\\&{}={\frac {2abc}{\sqrt {(a^{2}+b^{2}+c^{2})^{2}-2(a^{4}+b^{4}+c^{4})}}}.\end{aligned}}}$

on A és l'àrea del triangle i s és el semiperímetre

${\displaystyle s={\frac {a+b+c}{2}}.}$

La segona igualtat de més amunt és en essència la fórmula d'Heró.

Història

Segons Ubiratan D'Ambrosio i Helaine Selin, la llei esfèrica dels sinus es va descobrir al segle X, sent atribuida a Abu Mahmud Hamid ibn al-Khidr al-Khudjandi, Abu-l-Wafà Muhàmmad al-Buzajaní, Nassir-ad-Din at-Tussí i Abu-Nasr Mansur.^[1] El Kitab mayhulat qisi al-qura, (Llibre de les incògnites dels arcs de l'esfera) del segle XI d'Ibn Muadh al-Jayyaní conté la llei general dels sinus.^[2] La llei plana dels sins va ser enunciada més tard al segle XIII per Nasīr al-Dīn al-Tūsī. En el seu Sobre la figura del sector, va declarar la llei dels sinus per als triangles plans i esfèrics, i va proporcionar proves per a aquesta llei.^[3]

Exemples

Aquest és un exemple de com resoldre un problema emprant el teorema del sinus:

Donats: costat a = 20, costat c = 14, i angle C = 40 graus

Emprant el teorema del sinus, se sap que:${\displaystyle {\tfrac {a}{\sin A}}={\tfrac {c}{\sin C}}.}$

Introduint els valors donats a la fórmula, es troba que:${\displaystyle {\tfrac {20}{\sin A}}={\tfrac {14}{\sin 40}}.}$

Per tant, prenent l'arcsinus, l'angle A és igual a 66.67 graus.

El cas ambigu

Quan es fa servir el teorema del sinus per a resoldre triangles, si es donen unes condicions especials, existeix un cas ambigu on es poden construir dos triangles diferents (és a dir, hi ha dues solucions diferents possibles per al triangle).

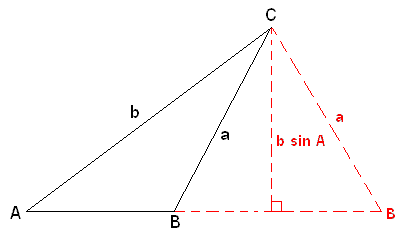
Donat un triangle genèric ABC, s'han de donar les següents condicions perquè es produeixi el cas ambigu:

• L'única informació coneguda del triangle és l'angle A i els costats a i b, on l'angle A no és l'angle contingut entre els dos costats (en la imatge de damunt, l'angle C és l'angle contingut entre els dos costats).
• L'angle A és agut (és a dir, A < 90°).
• El costat a és més curt que el costat b (és a dir a < b).
• El costat a és més llarg que l'altitud d'un triangle rectangle amb angle A i hipotenusa b (és a dir, a > b sin A).

En cas que totes les condicions anteriors siguin certes simultàniament, l'angle B pot ser agut o obtús; això significa que es poden donar els dos casos següents:

${\displaystyle B=\arcsin {b\sin A \over a}}$

O

${\displaystyle B=180^{\circ }-\arcsin {b\sin A \over a}}$

Demostració del teorema del sinus

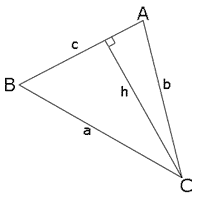
Es dibuixa un triangle amb costats a, b, i c, i angles A, B, i C. Es traça la perpendicular al costat c que passa pel vèrtex de l'angle C; per definició divideix el triangle original en dos triangles rectangles. Si la longitud sobre aquest segment és h.

Es pot observar que:

${\displaystyle \sin A={\frac {h}{b}}{\text{ i }}\sin B={\frac {h}{a}}.}$

Per tant

${\displaystyle h=b\,(\sin A)=a\,(\sin B)}$

i

${\displaystyle {\frac {a}{\sin A}}={\frac {b}{\sin B}}.}$

Fent el mateix amb la perpendicular traçada al costat a que passa pel vèrtex de l'angle A s'obté:

${\displaystyle {\frac {b}{\sin B}}={\frac {c}{\sin C}}.}$

Demostració completa:

Es dibuixa un triangle ABC de costats a, b, c i l'angle γ a C. Es troba el centre S de la circumferència circumscrita. Com que la circumferència passa pels tres vèrtexs, n'hi ha prou a trobar el punt d'intersecció entre les mediatrius de dos costats qualsevol del triangle (com que cada mediatriu és el lloc geomètric dels punts equidistants als dos extrems del costat, el punt on es tallen dues mediatrius és l'únic punt equidistant als tres vèrtexs). El costat c talla la circumferència k amb centre a S en dos arcs, l'arc on es troba el vèrtex C és l'arc capaç que veu el segment |AB| (és a dir el costat d del triangle) amb un angle γ i per tant el centre d'aquest arc veu el costat c amb un angle 2* γ (vegeu l'article arc capaç per a la demostració)

Per tant es pot observar que:

${\displaystyle \sin \gamma ={\frac {\frac {c}{2}}{r}}={\frac {c}{2r}},}$

I d'aquí

${\displaystyle {\frac {c}{\sin \gamma }}=2r\quad \left(\sin \gamma ={\frac {c}{2r}}\right)}$

Com que l'alçada del vèrtex B respecte de la base b és ${\displaystyle a\sin(\gamma )}$, l'àrea del triangle és:

${\displaystyle {\text{Area}}={\frac {1}{2}}ab\sin \gamma ={\frac {1}{2}}ab{\frac {c}{2r}}}$

D'aquí es dedueix que:

${\displaystyle {2r}={\frac {abc}{2{\text{Area}}}}.}$

Repetint el mateix procés per als angles α i β:

${\displaystyle {\frac {a}{\sin \alpha }}={\frac {b}{\sin \beta }}={\frac {c}{\sin \gamma }}={2r}={\frac {abc}{2{\text{Area}}}}.}$

Un teorema del sinus per tetraedres

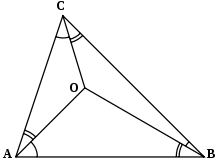
Un corol·lari del teorema del sinus tal com s'ha establert més amunt és que en un tetraedre amb vèrtex O, A, B, C, es té

${\displaystyle \sin \angle OAB\cdot \sin \angle OBC\cdot \sin \angle OCA=\sin \angle OAC\cdot \sin \angle OCB\cdot \sin \angle OBA.\,}$

Els dos cantons d'aquesta identitat es poden veure com a corresponents a les orientacions horària i antihorària de la superfície.

Posant qualsevol dels quatre vèrtexs en el lloc de O s'obtenen quatre identitats d'aquesta mena, però com a màxim tres d'aquestes són independents: si els costats "horaris" de tres d'aquestes identitats es multipliquen entre si, i el resultat s'iguala al producte dels costats "antihoraris" de les mateixes tres identitats, llavors, eliminant els factors comuns dels dos cantons resulta la quarta identitat. El motiu de l'interès d'aquesta relació d'"independència" és el següent: és conegut que tres angles són els angles d'algun triangle si, i només si, la seva suma és mitja volta. Quina és la condició necessària i suficient que han de complir 12 angles per poder formar algun tetraedre? Està clar que la suma dels angles de cada cara ha de ser mitja volta. Com que hi ha quatre cares triangulars, hi ha quatre restriccions per a les sumes dels angles, el nombre de graus de llibertat queda reduït de 12 a 8. Les quatre relacions donades per aquest teorema del sinus redueixen encara més el nombre de graus de llibertat, però no de 8 a 4 sinó de 8 a 5 atès que de les quatre restriccions només tres són independents. Així l'espai de totes les formes que poden tenir els tetraedres (sense importar la mida) és de dimensió 5. És a dir que es poden triar 5 angles arbitràriament (mentre cada un sigui menor de mitja volta) i sempre es podran trobar els altres 7 que formen juntament amb ells tots els angles d'un tetraedre.

Referències

Vegeu també

• Teorema del cosinus
• Teorema de la tangent
• Agrimensura

Enllaços externs

• PlainMath.Net-Area with sines Arxivat 2008-04-18 a Wayback Machine.
• Excellent tutorial on the law of sines Arxivat 2008-05-16 a Wayback Machine.
• The Law of Sines at cut-the-knot
• Degree of Curvature
• PlainMath.Net- The Law of Sines Arxivat 2008-04-18 a Wayback Machine. Revisió del teorema del sinus